Torus-Bilder für n=13

Für das Torus-Problem gibt es nur Lösungen, wenn ggT (n,6) = 1, oder anders ausgedrückt, wenn n weder durch 2 noch durch 3 teilbar ist. Die ersten Lösungen (außer für n=1) gibt es also für 5, 7 und 11.

Jedoch gibt es für diese drei n nur "Standard-Lösungen". Damit meine ich Lösungen, bei denen die Dame auf der nächsten Zeile immer um dieselbe Anzahl von Spalten versetzt ist. Oder noch anders ausgedrückt: Lösungen, die affine Abbilder der identischen Permutation sind, die als Graf die Diagonale hat.

Die ersten Nicht-Standard-Lösungen gibt es für n = 13. Berücksichtigt man Kongruenz auf dem Torus, so gibt es 11 Lösungen, nämlich 3 Standard- und 8 Nicht-Standard-Lösungen. Die Bilder der 8 Nicht-Standard-Lösungen können Sie unten sehen.

Berücksichtigt man Ähnlichkeit von Lösungen, so hat man zwei Gruppen von je 3 ähnlichen Lösungen, während die letzten beiden jeweils allein einen Orbit bilden. Sie sind also kongruent zu ihren Abbildern unter zentrischer Streckung.

Geht man noch weiter und erlaubt affine Abbildungen, so sind die drei Standard-Lösungen äquivalent, und darüber hinaus die beiden letzten in der Tabelle ("3-er und 4-er Springer-Linie" und "Abhang").

Alle Lösungen sind dreh-symmetrisch, entweder für 90° oder für 180°-Drehungen. Ich habe die Lösungen so verschoben, dass das Dreh-Zentrum im Zentum des Quadrates liegt. Die Damen sind in verschiedenen Farben abgebildet, abhängig davon, wie weit die näheste Dame auf einer Nachbar-Zeile oder -Spalte entfernt ist.

Ich habe den Lösungen Namen gegeben, die unter den Bildern stehen. Da ich die Lösungen noch nirgends anders gesehen habe, sind diese Namen als Vorschläge zu sehen; haben Sie eine bessere Idee, dann teilen Sie mir dies bitte mit.

Erste Gruppe
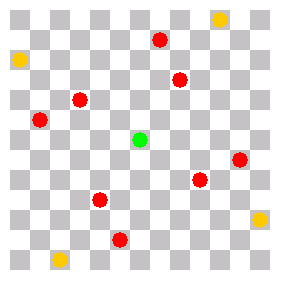
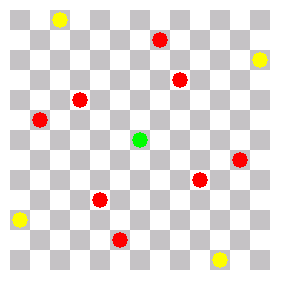
Quadrat mit 3-er Abstand an der Ecke	Quadrat mit 4-er Abstand an der Seite	2-3-Quadrat
Zweite Gruppe
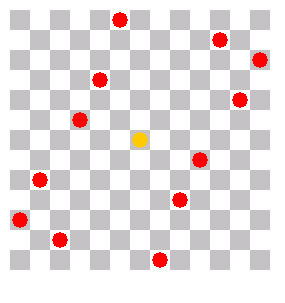
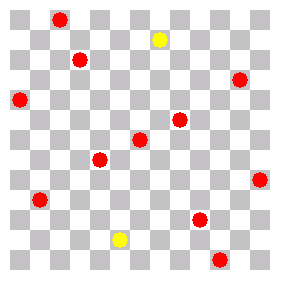
Aufgebogenes Rechteck (um es zu schließen, müssen Sie (5/0) eine Spalte nach rechts und (7/12) eine nach links schieben)	Flache Diagonale	Schiefes Oval
Dritte Gruppe (mit nur einer Lösung)
	3-er und 4-er Springer-Linie (die 4-er-Line startet oben rechts bei (11/3), geht zwischen (12/5) und (0/7) über den Rand und endet bei (1/9))
... und schließlich die vierte Gruppe (wieder mit nur einer Lösung)
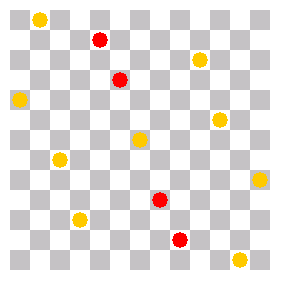
	Abhang (lange Linie von (1/0) über (4/1), (5,3), (6/6), (7/9), (8,11) bis zu (11,12))