Images for n=13

For the torus problem, solutions exist only if gcd (n,6) = 1; that means, only if n is divisible neither by 2 nor by 3. So, the first solutions (except for n=1) are for 5, 7 and 11.

However, for these three numbers there are only the "standard" solutions: by that I mean solutions where you get the queen in the next row by proceeding a constant number of columns. Or in other words: standard solutions are affine images of the unity permutation whose graf is the diagonal.

The first non-standard torus solutions arise with n = 13. There are, with respect to congruency on the torus, 11 solutions: 3 standard and 8 non-standard. You see images of these 8 below.

Using the concept of similarity of solutions, we have two groups of 3 solutions which are similar while the other two form an orbit alone, i.e. they are congruent to their extensions.

The solutions have all some symmetry, either for 90° rotation or for 180°. I shifted the solutions so that the center of rotation is in the center of the image. The queens are in differnt colors, depending on how far the nearest queen is in a neighbor row or column.

I gave names to the solutions which are written under the images. As I saw the solutions never elsewhere, these names are preliminar. If you have a better idea for the names, please let me know.

First group
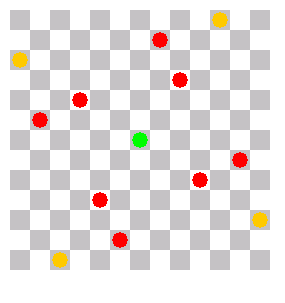
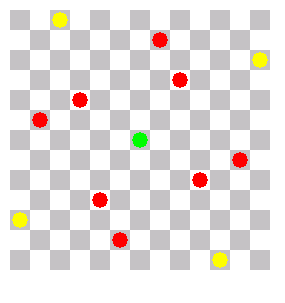
Square with 3-distance at corner	Square with 4-distance at edge	2-3-square
Second group
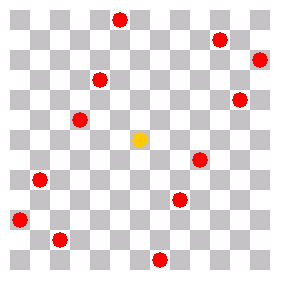
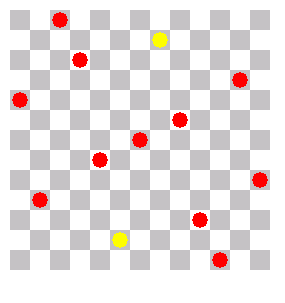
Opened rectangle (to close it, shift (5/0) right one column and (7/12) left)	Flat diagonal	tilted oval
Third group, containing only one solution
	3- and 4-knight line (the 4-line starts on the right at (11/3), crosses the border between (12/5) and (0/7), and ends at (1/9))
... and finally the fourth group, also containing only one solution
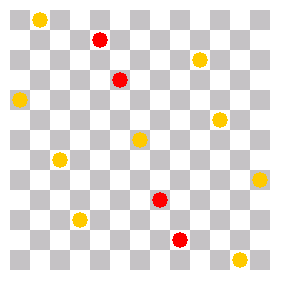
	Slope (long line from (1/0) via (4/1), (5,3), (6/6), (7/9), (8,11) to (11,12))