Minimal-Lösungen in alfabetischer Ordnung

Das Damen-Problem hat sehr viele Lösungen, zumindest, wenn das Brett immer größer wird.
Daher scheint es einfach, die erste Lösung zu finden. Aber es ist keineswegs einfach, es ist ziemlich schwer.
Natürlich müssen wir zuerst definieren, was wir mit "die erste Lösung" meinen. Gemeint ist eine alfabetische Reihenfolge der Lösungen. Zeile für Zeile notieren wir, in welcher Spalte eine Damen auf dem Brett steht. Bis n = 26 können wir diese Nummer durch den entsprechenden Buchstaben des Alfabets ersetzen; so erhalten wir ein (verallgemeinertes) Wort aus n Buchstaben. Die Reihenfolge der Lösungen entspricht dann genau der Reihenfolge, in der die entsprechenden Worte in einem Lexikon stünden. Wir nennen dies die "alfabetische Reihenfolge".
Der Grund dafür ist, dass die Lösungen nicht gleichmäßig über den gesamten Bereich der möglichen Lösungen verteilt sind. Die folgenden Bilder zeigen durch die Farbe eines Feldes an, wie viele Lösungen auf diesem Feld eine Dame haben. Die Bilder sind also zu interpretieren wie eine Temperatur-Karte der Wettervorhersage: Blau bedeutet sehr kalt, nur wenige Lösungen, Grün nicht ganz so kalt, aber die Anzahl bleibt unter dem Medianwert; Gelb bedeutet warm, die Anzahl der Lösungen liegt über dem Medianwert, und Rot bedeutet einen heißen Bereich, sehr viele Lösungen. Die vier Farben ändern auch noch ihre Intensität, für Blau und Grün zeigt hohe Intensität weniger Lösungen und für Gelb und Rot bedeutet eine größere Intensität mehr Lösungen. Wenn es überhaupt keine Lösung mit einer Dame auf dem Feld gibt, dann bleibt es leer.

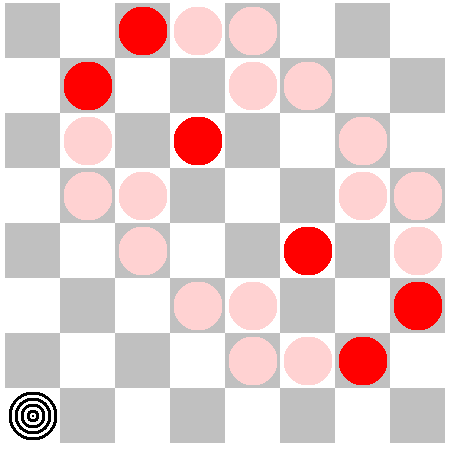


Für N8 sind die Anzahlen in der untersten Reihe: 4 / 8 / 16 / 18, und in den nächsten Reihen 8 / 16 / 14 / 8, dann 16 / 14 / 4 / 12, und 18 / 8 / 12 / 8. Das Verhältnis von höchster Anzahl (in der Mitte) zu kleinster (am Eck) ist 4,5.
Für N16 sind die Anzahlen in der untersten Reihe: 436.228 / 569.531 / 736.363 / 892.999 / 1.050.762 / 1.160.280 / 1.249.262 / 1.290.831. Bei steigendem n sollte die Verteilung gleichmäßiger sein, aber das Verhältnis von höchste zu kleinster Anzahl ist immer noch 2,96.
Betrachtet man diese Bilder, so sieht man, dass die erste Dame in der Ecke nur wenige Lösungs-Möglichkeiten zulässt. Das ist ungünstig für die Suche nach der kleinsten Lösung. Auch wenn es nur wenige Lösungen gibt, muss man doch viele Felder prüfen, und die meisten führen zu keiner Lösung. Noch deutlicher sieht man das an den Bildern, bei denen auf 0/0 schon eine Dame steht. Beim 8 mal 8 Brett gibt es dann keine Lösung mit der zweiten Dame auf 2/1 oder 3/1. Damen auf 0/1 oder 1/1 sind von den Regeln nicht erlaubt; es ist keine Überraschung, dass diese Felder leer sind. Aber bei den anderen beiden gibt es keinen offensichtlichen Grund fürs Leer-Bleiben.
Das entsprechende Bild für N16 zeigt, dass Damen auf 2/1 oder 3/1 möglich sind; aber auch hier sind es nur wenige Möglichkeiten. Es sind 16.346 Möglichkeiten für 2/1, verglichen mit 44.128 für 8/1.
Wenn wir weitere Damen setzen, ergeben sich folgende Bilder:



Eine ähnliche Zählung habe ich für das 24 mal 24 Brett gemacht, mit 7 vorab gesetzten Damen. Sind sie in Minimal-Position, dann gibt es 26 Lösungen, bei einer Zufalls-Position erhielt is 2.849.191 Lösungen. Das zeigt, wie dünn gesät die Lösungen im Minimal-Bereich sind.
Bekannte Minimal-Lösungen
Minimal-Lösungen waren im Jahr 2012 bis zur Größe 55 gefunden. Sie können sie in einem großen gif-Bild betrachten, das sie alle in einer Schleife anzeigt. Inzwischen (Stand Januar 2018) sind sie lückenlos bis 61 bekannt, danach noch etliche bis n=115.
Dr größte Teil der Suche wurde von Colin Pearson durchgeführt; er unterhält eine Web-Seite zu diesem Thema. Ab n=46 haben Wolfram Schubert und der Autor (M.Engelhardt) bei der Suche geholfen.
Im Herbst 2017 haben Matteo Fischetti und Domenico Salvagnin von der Univeristät Padua sich des Problems angenommen. Sie arbeiten mit Integer Linear Programming (ILP) und haben damit die Lösungen für 56 bis 61, alle weiteren ungeraden Zahlen unter 74, sowie 77, 79, 85, 91, 93, 97, 101, 103, 109 und 115 ermittelt.
Erstauhnlich ist, dass der Aufwand für die Suche nicht direkt an die Größe der Seite gekoppelt ist; zum Beispiel braucht 48 mehr Aufwand als jede Größe zwischen 49 und 55. Das scheint mit der Teilbarkeit der Zahl zu tun zu haben, aber wir haben keine weitere Erklärung dafür. Auf dieser Basis haben wir bis 2017 angenommen, dass die Suche nach der kleinsten 60 mal 60 Lösung eine große Herausforderung wird. Es hat sich aber gezeigt, dass dies nicht stimmt. Größe 48 ist immer noch die Größe, die den meisten Aufwand braucht. Matteo Fischetti und Domenico Salvagnin haben ein Papier zu diesem Thema geschrieben, Chasing First Queens by Integer Programming.
Die gefräßige Folge (greedy sequence)
Stellen Sie sich ein endloses Schachbrett vor; das heißt, die Zeilen und Spalten (oder auch Reihen und Linien) starten bei 1, aber enden nicht. Die Frage nach der kleinsten Damen-Lösung kann man auch für dieses Brett stellen. Die Nummern der Spalten dieser Minimal-Lösung sind die "greedy sequence", was wohl mit "gefräßige Folge" zu übersetzen ist; sie ist unter A065188 in der Encyclopedia of integer sequences enthalten. Lassen sie mich die Spalte der Dame in Zeile k als g(k) bezeichnen. (g als Abkürzung für "greedy").
Der Algorithmus zum Finden der Werte ist ganz simpel: man fängt mit der ersten Dame auf 1/1 an. Dann macht man Zeile für Zeile weiter, und nimmt jedesmal das erste erlaubte Feld. Damit ist dessen Spalte "verbraucht", oder "aufgegessen"; das ist wohl der Grund für den ungewöhnlichen Namen der Folge.
Die gefräßige Folge hat eine interessante Eigenschaft: sie ist eine Permutation der natürlichen Zahlen. Keine Spalte kommt mehrfach vor (die Abbildung ist injektiv), und jede Spalte kommt früher oder später einmal vor (die Abbildung ist surjektiv); das letztere erscheint einleuchtend, aber ist nicht so leicht zu beweisen.
Weil die Folge eine Permutation ist, kann man fragen, wie viele Spalten lückenlos besetzt sind, wenn die k-te Zeile ihre Dame bekommen hat. Diese Zahl bezeichne ich mit f(k). (f als Abkürzung für "filled"). Es ist klar, dass f eine monotone Abbildung ist. Meine Berechnungen zeigen, dass der Quotient k / f(k) gegen die Fibonacci-Zahl konvergiert, also gegen (sqrt(5) - 1) / 2 = 1.618034. Bisher habe ich noch keinen Beweis dafür.
Hier gebe ich Ihnen eine kleine Tabelle von Werten, die mich zur dieser Hypothese geführt haben (k / f(k) konvergiert gegen die Fibonacci Zahl); die letzte Spalte (Delta) enthält die Differenz zwischen aktuellem Wert und Grenzwert.
| k | g(k) | f(k) | k / f(k) | Delta |
| 50 | 32 | 32 | 1,5625 | 0,055534 |
| 100 | 162 | 62 | 1,639344 | -0,02131 |
| 200 | 323 | 124 | 1,612903 | 0,005131 |
| 500 | 310 | 311 | 1,607717 | 0,010317 |
| 1000 | 618 | 619 | 1,615509 | 0,002525 |
| 2000 | 3236 | 1236 | 1,618123 | -0,000089 |
| 5000 | 8089 | 3092 | 1,617076 | 0,000958 |
| 9999 | 16179 | 6179 | 1,618223 | -0,000189 |
Andere Start-Werte für die gefräßige Folge
Man kann eine gefräßige Folge auch mit anderen Start-Werten betrachten; das heißt, der Algorithmus ist der gleiche, die Folge ist immer noch "gefräßig", aber die ersten Werte sind anders.
Auch in diesen Fällen ist der Grenzwert derselbe. Das brachte mich zur Frage ob vielleicht auch die Folge selbst irgendwann gleich wird. Formal aufgeschrieben: ist h(k) die gefräßige Folge mit anderen Start-Werten, gibt es dann eine natürliche Zahl m so dass g(k) = h(k) für alle k > m. Ich war ein wenig enttäuscht, dass es offenbar nicht so ist, außer bei trivialen Konstellationen. Ein Beispiel für eine solche triviale Konstellation sind die Start-Werte h(1) = 2, h(2) = 4, h(3) = 1, h(4) = 3, h(5) = 5. Der Footprint dieser ersten 5 Damen auf die Spalten und auf die Diagonalen beider Richtungen ist in diesem Fall exakt derselbe; daher gibt es danach keine Abweichungen mehr.
In einigen Fällen habe ich lange Bereich von k gefunden wo g(k) und h(k) übereinstimmen; aber dann gabe es doch wieder eine Abweichung.