Mein Such-Algorithmus beim Damen-Problem T29

Im folgenden habe ich zusammengestellt, wie ich bei der Suche der Torus-Lösung für ein Schachbrett von 29 mal 29 Feldern vorgegangen bin. Einige Bermerkungen beziehen sich auch auf das Brett mit 31 mal 31 Feldern.

Zunächst ist mein Algorithmus auch ein Backtracking, so wie dies in einigen Lehrbüchern steht. Von dieser Ausgangs-Basis habe ich schrittweise Verbesserungen eingebaut.

Verbesserung 1: größere Vorausschau - nicht nur die nächste Reihe.

Die meisten Programm prüfen für die nächste Dame jeweils nur, ob in der nächsten Reihe noch ein Feld frei ist. Vermutlich empfehlen viele Vorlesungen dies auch, um den Aufwand für jeden einzelnen Schritt möglichst klein zu halten. Und wahrscheinlich stimmt dies beim Damen-Problem auch bei kleinen Schach-Brettern, etwa bis 12 mal 12. Hier investiert mein Programm mehr Arbeit:

• es führt ein n-mal-n-Array mit, in dem für jedes Feld vermerkt ist, von wievielen gesetzten Damen es erreicht werden kann. Mit diesem Array stellt es fest, ob in irgend einer noch nicht besetzten Reihe eventuell keine Felder mehr frei sind; ist dies der Fall, geht es gleich zurück.
• Wenn ich also auf einem 8-mal-8-Schachbrett vier Damen auf die Reihen 1 bis 4 gesetzt habe, und dadurch sind in Reihe 7 alle Felder "bedroht", dann setzt das Programm gleich die Dame in Reihe 4 weiter; es versucht nicht, Damen auf Reihe 5 und 6 zu setzen, was durchaus noch gehen kann.
• Der zweite Unterschied ist, dass das Programm die Reihen nicht unbedingt in der natürlichen Reihenfolge abarbeitet; stellt es in Reihe vier fest, dass es auf Reihe 7 nur noch zwei Möglichkeiten gibt, auf den Reihen 5, 6 und 8 aber noch drei oder vier Möglichkeiten, dann setzt es die nächsten Damen auf die Reihe 7.

Auf dieser Basis habe ich die ersten Berechnungen für das 25 mal 25 Feld durchgeführt.

Verbesserung 2: Spalten und Diagonalen für BackTrack nutzen.

Die anderen bisherigen Damen-Programme, die ich kenne, gehen alle Reihen des Schach-Brettes durch. Das ist aber nicht notwendig. Es kommt nur darauf an, die Fall-Unterscheidungen für alle übrigen Fälle so zu treffen, dass das Programm wirklich alle Möglichkeiten erfasst. Und für solche Fall-Unterscheidungen eignen sich die Spalten genau so gut wie die Reihen. Zusätzlich eignen sich beim Torus-Problem auch noch die Diagonalen und die Anti-Diagonalen (Diagonalen sind die Linien, auf denen x - y konstant ist, Anti-Diagonalen die zu x + y konstant).

Dabei kann die Reihenfolge dieser Fall-Unterscheidungen ganz dynamisch von den bisher schon gesetzten Damen abhängen.

Ich bin überzeugt, dass diese Verbesserung einen deutlichen Vorteil bringt; allerdings habe ich dies nicht genau geprüft, da ich diese Verbesserung gleichzeitig mit der nächsten eingebaut habe.

Verbesserung 3: Vermeiden von Index-Rechnungen, Verketten der Nachbar-Felder.

Ich habe mein Programm (auch) als Übungs-Programm für die Programmier-Sprache Java geschrieben; irgendwann hatte ich den Verdacht, dass die vielen Index-Rechnungen das Programm langsam machen; außerdem wurde es allmählich kompliziert.

An dieser Stelle habe ich dann einen Schritt in Richtung Objekt-Orientierung getan und für die Felder eine Klasse QField sowie für die Linien (Reihen, Spalten und (Anti-)Diagonalen eine Klasse QLineInfo geschrieben. Alle notwendigen Instanzen werden am Anfang des Programmes angelegt und entsprechend verkettet. Während der Berechnungen werden lediglich die QField-Instanzen auf aktiv oder passiv gesetzt und aus der Liste der noch zu betrachtenden Felder ein- oder ausgekettet.

Wie oben gesagt, habe ich dies zusammen  mit dem Nutzen von Spalten und Diagonalen implementiert; insgesamt eine deutlich Verbesserung, die ich aber nicht wirklich auf die beiden Schritte aufteilen kann.

Verbesserung 4: Möglichkeiten zur Aufteilung schaffen.

Das Programm versteht ein paar Kommandos. Dies sind im Einzelnen:

Setzen einer festen Dame

Mit "Set 1 1" bewirke ich, dass für den Programm-Lauf von vornherein eine Dame auf Feld 1/1 gesetzt wird. Es können mehrere solche Set-Kommandos verarbeitet werden, allerdings sollten sie sich nicht widersprechen.

Blockieren eines Feldes

Mit "Block 1 1" bewirke ich, dass im ganzen Programm-Lauf keine Dame auf Feld 1/1 gesetzt wird. Auch hier können mehrere Block-Kommandos verarbeitet werden.

Festlegen einer Mindest-Distanz zwischen den Damen

Mit "MinDist 4" bewirke ich, dass das Programm Dame auf Nachbar-Linien nicht zu nahe aneinander setzt. Linie ist hier im Sinn von Reihe und Spalte gemeint, Diagonalen zählen hier - anders als oben - nicht mit. Steht zum Beispiel auf Feld 7/11 eine Dame, so können bei MindDist 4 auf den Feldern 6/8, 6/9, 6/13, 6/14, 8/8, 8/9,8/13, 8/14, 4/10, 5/10, 9/10, 10/10,  4/12, 5/12, 9/12 und 10/12 keine Damen stehen. Dieses Kommando kann nur einmal in einem Lauf gegeben werden.

Beachten Sie, dass dieses Kommando dynamisch wirkt: mit jeder neu gesetzten Dame werden die entsprechenden Felder gesperrt; beim Wegnehmen der Dame im BackTracking wieder freigegeben. Der Aufwand für jeden einzelnen Schritt wird größer; insgesamt geht der Lauf aber deutlich schneller, weil er ja auch nur nach wenigeren, speziellen Lösungen sucht.

Festlegen einer sekundären Mindest-Distanz

Mit "SecMinDist 7" bewirke ich, dass das Programm einen weiteren Mindest-Abstand einhält, wenn es schon ein Paar Damen im Mindest-Abstand hat. Auch dieses Kommando macht nur einmal in einen Programm-Lauf Sinn.

Als Beispiel dazu: mit "MinDist 2" (das ist der Standard-Wert) und "SecMinDist 7" und mit Damen auf 7/11 und 8/13 sperrt das Programm die Felder 6/5, 6/6, 6/7, 6/8, 6/9 auf der einen Seite des MinDist-Paares, sowie 9/15, 9/16, 9/17, 9/18 und 9/19 auf der anderen Seite.

Vermeiden einer Springer-Linie

Mit "NoKniLine" bewirke ich, dass das Programm nie drei Damen in einer "Springer-Linie" setzt, zum Beispiel auf 3/5, 5/6 und 7/7. Senkrecht zu den ersten beiden Damen - also im Beispiel auf 4/8 oder 6/4 - darf aber eine Dame stehen.

Vermeiden von mehreren Springer-Nachbarinnen

Mit "SingleKnight" verbietet das Programm bei zwei Damen im Springer-Abstand auch weitere Nachbarinnen in senkrechter Richtung.

Verbesserung 5: Aufteilen und Zusammensetzen.

Um die Gesamt-Suche Aufteilen und die Ergebnisse zusammensetzen zu können, muss ich die Lösungen in einer Datei speichern. In weiteren Programmen fasse ich dann die gefundenen Lösungen in weiteren Dateien zusammen zusammen und scheide aus, was in den vorhergehenden Schritten doppelt oder mehrfach gefunden wurde.

Natürlich ergibt sich sehr schnell eine viel zu große Zahl von Lösungen. Um die Aufgabe trotzdem effektiv zu lösen, muss man übergehen zu sinnvollen Repräsentaten. Dies ergibt sich mehr oder weniger natürlich aus den Symmetrien, die ich betrachte.

Verbesserung 6: Ausnutzen von Symmetrien.

In spezielleren Fällen ist dies sicher schon oft geschehen. Die meisten Programme nutzen allerdings nur die aller-elementarste Spiegel-Symmetrie. Sie setzen als beim normalen, klassischen 8 mal 8 Brett die erste Dame nur in die linke Hälfte und multiplizieren am Ende die Zahl mit zwei.

Einen Schritt weiter ist in dieser Richtung Hr.U.Schimke gegangen. Mit ihm habe ich ein paar E-Mails gewechselt. Sein Programm erkennt auch, ob es sich bei einer neu gefundenen Lösung um das gedrehte Abbild einer Lösung handelt, die vorher schon gezählt wurde.

Durch das Abspeichern und spätere Auswerten der Lösungen kann ich diesen Teil, der das Programm doch etwas komplexer macht, auslagern.

Bei der Suche nach Torus-Lösungen sind dann natürlich noch die Verschiebungen zu berücksichtigen. Das reduziert die Größe des Feldes, das zu durchsuchen ist, erheblich.

Für die intensivere Anwendung von Symmetrien ist etwas Gruppen-Theorie gut. (Hier folgt noch ein Verweis auf das Buch von A.Kerber; an dessen Sprechweise schließe ich mich an).

Alle Symmetrien, die ich bisher betrachtet habe, ergeben sich aus Gruppen von Bewegungen, die das zugrunde liegende Schachbrett in sich überführen. Bei den allereinfachsten Symmetrien besteht die Gruppe nur aus der Identität und der vertikalen Spiegelung, ist also isomorf zu 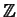₂. Die nächste Stufe, die auch Hr.Schimke für die "normalen" Damen betrachtet hat, besteht zusätzlich aus der horizontalen Spiegelung und aus den 90° Drehungen. Diese Gruppe ist die dihedrale Gruppe D₄. Dies ist gleichzeitig die Gruppe der kongruenten Abbildungen im gegebenen "Rand" des Schachbrettes, also ohne Verschiebungen.

Für die Torus-Damen kann man einfach die Gruppe aller Verschiebungen betrachten, mathematisch gesproche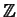n _n × 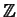_n. Dies ist am Ende des Artikels von Rivin, Vardi und Zimmermann auch angedeutet.

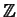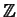Natürlich ist es jedoch, diese beiden Gruppen zusammenzunehmen. Damit betrachte ich alle kongruenten Abbildungen auf dem Torus. Dabei kommen dann auch kompliziertere Symmetrien in Betracht, wie zum Beispiel die Zusammensetzung einer Spiegelung mit einer Verschiebung. Gruppen-theoretisch handelt es sich dabei um ein Kranz-Produkt von D₄ mit _n × _n.

Eine Figur heißt dann symmetrisch bezüglich einer Bewegung, wenn sie durch diese Bewegung in sich selbst überführt wird. Oder in der Sprechweise der Gruppen-Theorie: wenn die Bewegung im Stabilisator der Figur liegt.

Die Menge aller Lösungen zerfällt in dieser Betrachtung in die Orbits der betrachteten Gruppe. Die Suche nach allen Lösungen reduziert sich damit darauf, eine Transversal-Menge aller Lösungen bezüglich der betrachteten Gruppe zu finden.

Für die Suche nach den T29-Lösungen habe ich genau dies getan. Um einfach entscheiden zu können, habe ich jede gefundene Lösung umgesetzt auf die lexikalisch kleinste Lösung im zugehörigen Orbit; diese Lösung habe ich dann gespeichert. Wie dies im Einzelnen geschah siehe unten bei Schritte für Torus-kongruente Lösungen.

Verbesserung 7: Weitere, größere Gruppen.

Inzwischen habe ich auch noch weitere Gruppen betrachtet, die das Schachbrett in sich selbst überführen. Zunächst kann man zu den kongruenten Bewegungen die ähnlichen Bewegungen hinzunehmen; eine "zentrische Streckung" ist auch bei den endlichen Mengen sinnvoll möglich, wenn der Streck-Faktor k teilerfremd ist zur Größe des Schachbrettes n. Weiter kann man alle affinen Abbildungen betrachten oder auch die speziellen affinen Abbildungen mit einer Determinante von 1 oder -1.

Mit den ähnlichen Abbildungen ergibt sich das folgende Vorgehen:

• 1) Zuerst besorge ich mir eine Transversal-Menge aller "Halsbänder" (= engl. Necklaces, natürlich im mathematischen Sinn gemeint).
• 2) Dann beginne ich bei den Halsbändern mit vielen Perlen (beads); ich gehe diese Halsbänder durch und setze, dem Halsband entsprechend, Damen auf die "Springer-Linie" (k, 2k). Bei den n, für die es Torus-Lösungen gibt, führt dies zu keinen Konflikten.
• 3) Jede solche Teil-Lösung versuche ich auf alle Arten zu einer vollen Lösung zu ergänzen. Dabei vermeide ich aber Lösungen, die auf irgend einer anderen Springer-Linie zu einem schon verarbeiteten Halsband führen.

Auf diese Art komme ich am Schluss dazu, alle Lösungen zu finden, die auch auf allen Springer-Linien nur eine Dame haben.

Habe ich so alle Lösungen eingesammelt, so kann ich daraus eine Transversal-Menge bezüglich Torus-Kongruenz + Ähnlichkeit machen. Aus dieser kann ich mir dann eine Transversal-Menge bzgl. Torus-Kongruenz ableiten oder auch direkt die interessanten Zahlen ausrechnen.

Diesen 7.Schritt habe ich bei der Suche nach den T31-Lösungen erfolgreich angewendet.

Schritte für Torus-kongruente Lösungen, T29.

Als erstes habe ich Lösungen gesucht, die midestens drei Damen in einer "Springer-Reihe" haben. Also im Programm die Anweisungen:
Set 1 1
Set 2 3
Set 3 5

Damit die Läufe nicht zu groß werden, habe ich noch eine Dame auf ein mögliches Feld in der vierten Reihe gesetzt. Andererseits habe ich Felder blockiert, um die Springer-Reihe wirklich mit 1/1 beginnen zu lassen und um Fälle zu vermeiden, deren Spiegelbild ich schon habe. Das ergibt zum Beispiel (für T29) die vollständige Kombination
Set 1 1
Set 2 3
Set 3 5
Set 4 10
Block 29 28
Block 29 27
Block 29 26

Danach habe ich nach den Lösungen gesucht, die zwei Damen im Springer-Abstand haben, aber nicht in einer Springer-Reihe. Diese habe ich weiter unterteilt danach, ob eine der Damen noch eine weitere "Springer-Nachbarin" hat, die in senkrechter Richtung zur ersten steht. Hat sie das, so sortiere ich sie ein unter "NoKnightLine", hat sie das nicht, dann unter "SingleKnight". Im letzteren Fall habe ich dann noch mit secMinDist gearbeitet.

Beispiel für Parameter bei SingleKnight:
Set 1 1
Set 2 3
Set 3 7
SecMinDist 4
SingleKnight
eventuell ergänzt um weitere feste Damen, die allerdings nur zur Aufteilung dienten.

Beispiel für Parameter bei NoKnightLine:
Set 1 1
Set 2 3
Set 4 2
NoKniLine
ergänzt um eine weitere feste Damen auf Reihe 3, die allerdings nur zur Aufteilung dient.

Schließlich habe ich nach den Lösungen gesucht, die einen größeren Mindest-Abstand haben, eingeordnet unter "MinDist".

Diese Läufe hatten beispielsweise die Kommandos
Set 1 1
Set 2 5
Block 29 26
MindDist 4
eventuell mit weiteren Unterteilungen.