Konflikte im Damen-Problem

Ein Konflikt.

Das Damen-Problem vermeidet Konflikte zwischen den Schach-Damen; das ist ja gerade die Definition.

Wenn hier trotzdem von Konflikten die Rede ist, so beruht dies auf einer Veränderung der Sichtweise. Dabei sollen das "normale" Damen-Problem und die Torus-Variante unter einen Hut kommen. Der springende Punkt ist: wir betrachten die normalen Lösungen als Torus-Lösungen mit Fehlern. Und diese Fehler sind genau die "Konflikte", um die es hier geht.

Ein wenig formaler: zwei Damen bilden einen Konflikt, wenn sie auf derselben Torus-Diagonalen oder Torus-Anti-Diagonalen stehen. Und noch formaler: ist p eine Permutation von {0 .. n-1}, i und k verschieden, 0 ≤ i,k < n, und ist p(i) - i = p(k) - k (mod n) oder p(i) + i = p(k) + k (mod n), dann bilden die beiden Punkte (i, p(i)) und (k, p(k)) einen Konflikt.

Damit sind Konflikte für alle Permutationen definiert. Im weiteren geht es aber immer nur um Permutationen, in denen maximal 2 Damen auf einer (Anti-)Diagonale stehen.

Mit dieser Definition kann man sagen: eine Torus-Damen-Lösung ist eine Permutation, die keine Konflikte hat.

Ein Konflikt kommt selten allein

Lösungen des normalen Damen-Problems haben normalerweise Konflikte. Natürlich sind Torus-Lösungen auch Lösungen des normalen Damen-Problems. Andere Lösungen haben gemäß Definition immer mindestens einen Konflikt.

Überraschend ist, dass es vermutlich keine Lösungen mit nur einem Konflikt gibt. Der Autor meint, einen Beweis dafür zu haben, ist sich aber noch nicht ganz sicher. Insofern ist es noch eine offene Frage. Falls jemand ein Beispiel für eine normale Lösung mit nur einem Konflikt hat, oder auch einen Beweis dafür, dass es das nicht geben kann, dann bitte an mich schicken.

Torus-Lösungen gibt es nur dann, wenn n weder durch 2 noch durch 3 teilbar ist. Schaut man sich den Beweis dazu an, so sieht man, dass die Argumentation separat für die Diagonalen und die Anti-Diagonalen gilt. Mit dieser Methode kann man zeigen, dass es für ein gerades n sowohl einen Konflikt bei den Diagonalen als auch einen bei den Anti-Diagonalen gibt. Damit sind es mindestens zwei Konflikte. Jedoch könnte es Lösungen mit nur einem Konflikt geben, wenn n ungerade ist. Bis zum 18 × 18 Brett taucht jedoch keine solche Lösung auf.

Ein Konflikt lässt sich auflösen; der Bereich dafür sieht aus wie die Beweis-Figur für die binomische Formel (a + b)² = a² + 2ab + b².

Konflikte auflösen

Echte Torus-Lösungen lassen sich horizontal und vertikal verschieben. Bei normalen Lösungen geht das nicht, zumindest nicht immer. Aus der Sichtweise, dass eine normale Lösung Konflikte hat, stellt sich das so dar: man muss die Verschiebung so wählen, dass beide Teile des Konflikts durch eine Randlinie durchbrochen werden. Dann sind die Damen getrennt (ich sage auch: separiert), der Konflikt ist aufgelöst.

Mit Verschieben kann man jeden einzelnen Konflikt auflösen. Den Bereich der Punkte, die nach Verschiebung auf den Ursprung einen separierten Konflikt ergeben, bezeichne ich als den Trenn-Bereich oder Separations-Bereich des Konfliktes.

Stellt man sich das in der endlosen, periodischen Ebene vor, so kann man aus einem Konflikt eine Figur zeichnen, die an die geometrischen Begründung der binomischen Formel (a + b)² = a² + 2ab + b² erinnert. Die beiden Quadrate lassen den Konflikt bestehen, die beiden Rechtecke lösen ihn auf.

Konflikt-Konstellation

Zwei Konflikte, fünf unbeteiligte Damen.

Alle Damen einer normalen Lösung, die an einem Konflikt beteiligt sind, bilden zu­sammen die Kon­flikt-Kon­stel­lation der Lösung. Eine Kon­flikt-Kon­stel­lation ist also eine Unter­menge der Punkte eines Grafen einer Per­mutation, und zwar eine Unter­menge mit besonderen Eigen­schaften. Jeder normalen Damen-Lösung kann man eindeutig ihre Konflikt-Konstellation zuordnen. Für Torus-Damen-Lösungen ist die Konflikt-Konstellation die leere Menge.

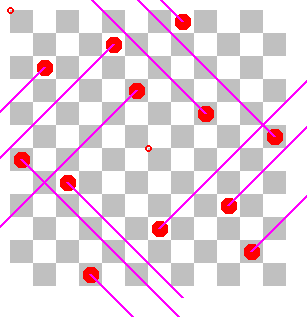
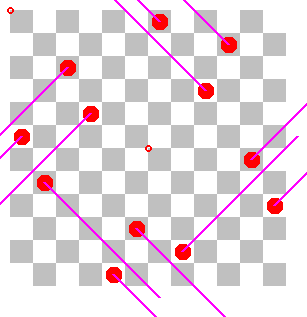
Normalerweise ist die Kon­flikt- Kon­stel­lation einer Lösung eine echte Teil­menge aller Damen. Das zeigt das Bild links. Es kommt aber auch der Fall vor, dass alle Damen an Konflikten beteiligt sind und die Kon­flikt-Kon­stel­lation schon die ganze Lösung darstellt. Erstmals ist es bei den Lösungen für das 4×4 Brett so, und danach erst wieder beim 12×12-Brett. Dort gibt es vier Lösungen (bis auf Drehen und Spiegeln), die hier angegeben sind. Auch die Konflikt-Linien sind eingezeichnet; sie sind allesamt durch den Rand unterbrochen, so dass wir echte Lösungen des normalen Damen-Problems haben.

Alle Damen sind an Konflikten beteiligt - Lösung 3.

Die Abbildung Damen-Lösung auf Konflikt-Kon­stel­lation ist normaler­weise weder injektiv noch surjektiv. Anders ausgedrückt: manchmal kann eine Konflikt-Konstellation auf verschiedene Art und Weise zu einer Lösungs-Permutation ergänzt werden, und manchmal kann man sie überhaupt nicht ergänzen.

Alle Damen sind an Konflikten beteiligt - Lösung 13.

Alle Damen sind an Konflikten beteiligt - Lösung 362.

Alle Damen sind an Konflikten beteiligt - Lösung 606.

Größen für eine Klassifizierung

Für eine Klassifizierung der Damen-Lösungen nach ihren Konflikt-Kon­stel­lation sind vier Größen interessant. Für die dritte und vierte davon verwendet der Autor ein wenig Grafen-Theorie. Die an Konflikten beteiligten Damen bilden einen Grafen; Ecken des Grafen sind eben diese Damen, und eine Kante besteht genau dann, wenn die beiden Damen zum gleichen Konflikt gehören. Einfacher ausgedrückt: eine Kante zwischen zwei Damen gibt es genau dann, wenn die beiden Damen auf derselben Torus-Diagonale oder Torus-Anti-Diagonale stehen.

Da es nur die beiden Diagonal-Richtungen gibt, hat der Graf maximal Grad 2 (Grad bezeichnet die "Verzweigungs-Zahl" an einer Ecke, d.h. die Anzahl Kanten, die von dieser Ecke ausgehen). Eine Konflikt-Konstellation kann durchaus zu einem zyklischen Grafen führen. Jedoch ist dem Autor kein Fall bekannt, in dem man einen zyklischen Grafen zu einer Damen-Lösung ergänzen kann, oder ihn auch nur so verschieben kann, dass alle Konflikte aufgelöst sind. Dies ist ein weiteres offenes Problem.

Nun zurück zu den angekündigten vier Größen. Diese sind:

• Die Anzahl der Konflikte.
• Die Anzahl der Damen, die an Konflikten beteiligt sind.
• Die Anzahl der Zusammenhangs-Komponenten des Konflikt-Grafen.
• Die maximale Größe einer Zusammenhangs-Komponenten des Konflikt-Grafen.

Tabellen zu den bisher bekannten Größen sind auf der folgenden Seite zusammengestellt.

Nimmt man eine fünfte Größe hinzu, die Anzahl der zyklischen Zusammenhangs-Komponenten, dann besteht zwischen diesen Größen die folgende Beziehung:

 
 Anzahl beteiligter Damen =    Anzahl Konflikte
                             + Anzahl Zusammenhangs-Komponenten
                             - Anzahl zyklische Zusammenhangs-Komponenten
                             

Dieser Zusammenhang spiegelt sich jedoch nicht in den Tabellen wieder.

  Start of page