Die nächsten Ziele: Q28 und T35

Unterwegs in Japan zum Weltrekord: Q28

In Japan ist ein Team (Yuuma Azuma, Hayato Sakagami, Kenji Kise vom Tokyo Institute of Technology) unterwegs, den nächsten Meilenstein zu erreichen; siehe diesen Artikel. Einer aus dem Team, Kenji Kise, hat schon 2004 die falsche Zahl für Q24 korrigiert, wenn es nicht hier eine Names-Gleichheit gibt.

Dr.Thomas Preußer schrieb mir Ende 2018, dass geschilderte Vorgehen ganz plausibel ist; inzwischen ist über ein Jahr vergangen - ich bin gespannt, wann das Ziel erreicht ist! Auf der Web-Seite habe ich dazu noch nichts gefunden.

Auf der Torus-Seite: T35

Seit einiger Zeit arbeite ich daran, die Zahl auch für T35 zu ermitteln. Meine Näherungs-Formel (siehe Artikel An Easy Counting Lemma) gibt einen Wert von 9,66 Billiarden, gefunden waren am davon bisher nur 53.742.116.622.600 (ca 54 Billionen), was 0,55 Prozent entspricht.

Generelles Vorgehen

• Eine geordnete Liste der (mathematischen) Halsbänder (Necklaces) erstellen, zumindest den Anfang. Für n=35 besteht die Liste aus 342.476 Halsbändern, die wenige als 11 Perlen (beads) haben. Für größere Halsbänder erfolgt dann eine Sonder-Behandlung (Cut, siehe unten).
• Tabelle möglicher Skelette dazu erstellen. Ist die Anzahl in einem Zweig zu groß, dann wird auch hier auf eine Sonder-Behandlung umgeschaltet. Für n=35 ergaben sich 7.467.085 aus 10.609 Halsbändern, die weniger als 8 Perlen (beads) haben. Für größere Halsbänder erfolgt dann eine Sonder-Behandlung; sie startet mit den 28.260 8-Perlen-Halsbändern und erlaubt, dass noch größere Halsbänder entstehen.
• Bearbeiten der Fälle, in denen die Skelette nicht weiter verzweigt wurden; ich nenne sie "Cut-Fälle", weil das Weiter-Verzweigen abgeschnitten ist. Dies noch unterteilt nach den kleinen Fällen mit mehr vorbelegten Damen und den großen (wenige vorbelegte Damen).
• Filtern und Sortieren der Lösungen, die das eigentliche Skelett überschreiten; sie sind im vorherigen Schritt entstanden.
• Aufnehmen der zusätzlichen Skelette und Lösungen in die Datenbank.
• Suche für die normalen Skelette, bei denen eine Verzweigung (das meint mögliche Erweiterungen) schon beim Erstellen der Skelette durchgeführt wurde. Dies wieder unterteilt nach großen und kleinen Fällen.
• Einmal über die komplette Datenbank gehen: Symmetrie-Faktoren ermitteln, wenn benötigt, und alles Zusammenzählen.
• Tests dazu. Wie diese gedacht sind, ist ein eigenes Kapitel.

Die Suche erfordert einen großen Rechen-Aufwand; das Projekt wird von der Lino GmbH unterstützt, die einen Server in der ungenutzten Zeit zur Verfügung stellt. Ansonsten arbeitet mein Rechner daran; es kann noch Jahre dauern. Die Suche erfolgt im Hintergrund, sie stört die normale Arbeit am Rechner kaum, und sie kann auch relativ einfach unterbrochen und später fortgesetzt werden.

Zeitlicher Ablauf

• Seit 2017: Entwurf und Implementieren der Programme für das Vorgehen; Test mit den kleineren Größen.
• 2019-08-25: Beginn mit n=35, Suche nach den Skeletten
• 2019-08-28: Anlegen der vorläufigen Datenbank mit 7.467.085 Einträgen
• 2019-10-24: Suche nach den Lösungen mit großen Armbändern (mindestens 8 Perlen) ist fertig; 290.169.786 Lösungen gefunden, die erst noch normiert und sortiert werden müssen.
• 2020-03-07: die Cut-Behandlung der "kleinen" Zweige ist fertig. Beginn der Suche der großen Cut-Fälle (nur wenige vorbelegte Damen).
• 2020-04-07: erster Such-Lauf auf einem Lino-Rechner startet.
• 2020-07-04: erster Such-Lauf auf einem Lino-Rechner erfolgreich zu Ende; zweiter startet.

Einzelne Punkte, die während der Suche auftauchten

Wie umgehen mit den Skeletten?

Der Weg für eine effiziente Suche sollte über die Skelette im Bezug auf Halsbänder gehen - alles natürlich im mathematischen Sinn. Auch habe ich daran gedacht, dass ein großer Teil der Suche auf FPGA erfolgt. Leider ist dieser Weg wohl zu kompliziert, um es effizient auf FPGAs zu implementieren. Deswegen läuft das Programm bisher vollständig auf herkömmlichen PCs.

Inzwischen verfolge ich parallel die Idee, statt der Halsband-Skelette mit Linien-Skeletten zu arbeiten; eine Erklärung dazu will ich später liefern. Grob geht es bei den Halsband-Skeletten um Linien, auf denen möglichst viele Damen in einer vorgegebenen Ordnung stehen. Bei den Linien-Skeletten geht es nur um die Linien, auf denen möglichst viele Damen stehen; die Anordnung der Damen auf diesen Linien spielt keine Rolle.

Das Ermitteln des Halsband-Skeletts ist aufwendig; vielleicht muss ich aber nur meine Implementierung weiter verbessern. Ein anderer Ansatz ist, erst das Linien-Skelett zu ermitteln und dann erst aus diesem das Halsband-Skelett. Bisher geht das Ermitteln des Linien-Skeletts um eine großen Faktor schneller: bei T23 beträgt er 244, bei T25 sogar 324.

Der Nachteil: es gibt viel mehr Linien-Skelette als Halsband-Skelette. Um eine Größen-Vorstellung zu bekommen, habe ich Grafiken erstellt, die die Anzahl der Lösungen abhängig von der Größe des Skeletts zeigen; dies für die beiden Varianten Linien- und Halsband-Skelett.

Verteilung der Lösungen, abhängig von der Größe des Skeletts.

Die ersten Lösungen zu "großen" Fällen.

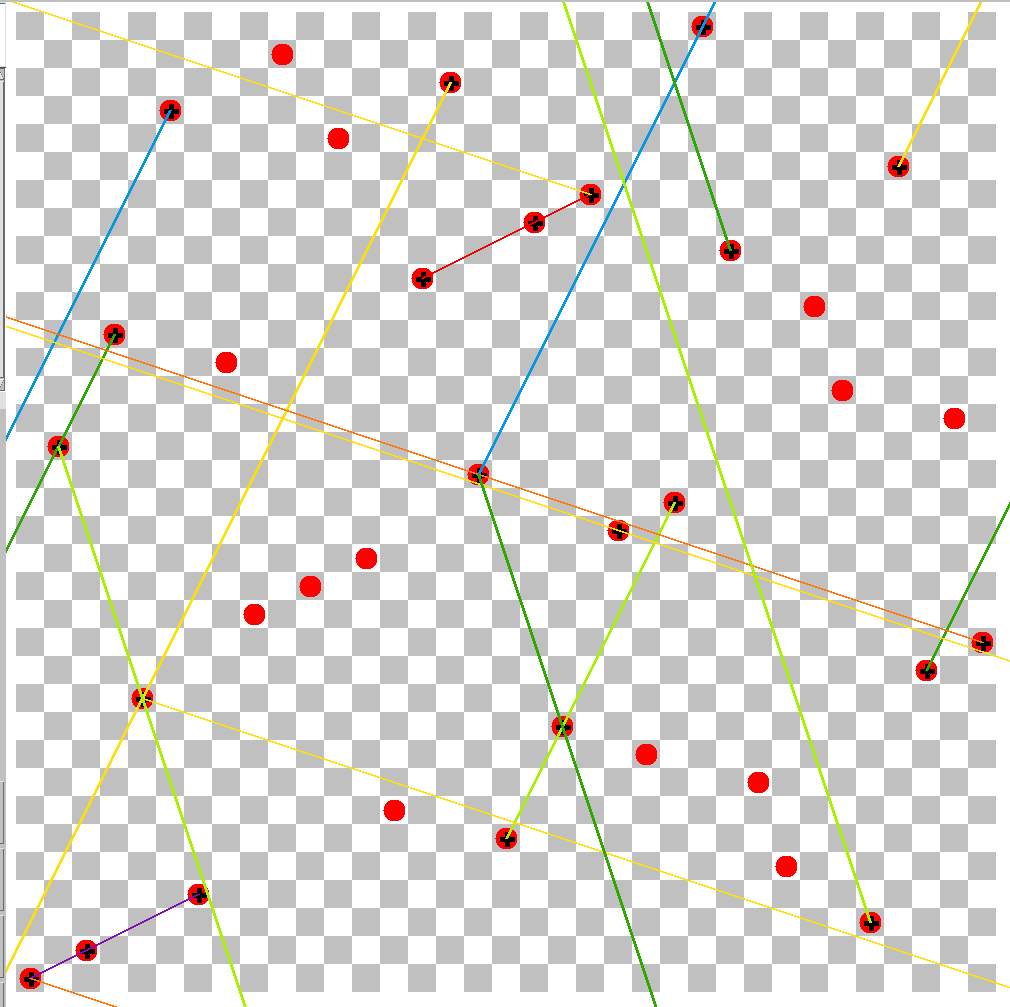
Sie gehören zum Halsband 0-1-3; es ist vorbelegt mit den Damen auf 0/0, 2/1 und 6/3. Die Damen, die jeweils zum Skelett gehören, tragen ein schwarzes Plus-Zeichen. Mit farbigen Linien sind noch einige weitere Springer-Linien mit drei Damen in einer Position, die diesem Halsband entspricht, eingezeichnet, zum Beispiel im linken Bild 17/5, 19/9 und 23/17 (hellgrüne Linie). Da ist das Halsband auf 0-2-6 gestreckt.

Man sieht auch, dass die drei Damen auf 8/13, 10/14 und 12/15 auf einer Springer-Linie stehen; diese Position gehört aber zum kleineren Halsband 0-1-2, deswegen gehören diese Damen nicht zum Skelett.