Links
back to main page "WorldRecord"..
Other languages
Next goals: Q28 and T35
On the way to world record Q28 in Japan
In Japan, ateam (Yuuma Azuma, Hayato Sakagami, Kenji Kise of the Tokyo Institute of Technology) started for the next mile stone; see this article. One of the team, Kenji Kise, has corrected the wrong number for Q24, back in 2004, if I am not mislead by a contigous equality of the name.
Dr.Thomas Preußer informed me in the end of 2018, saying that the descripted method is quite feasible; meanwhile, more than a year has gone - I am curious about it! On their page, I could not find an information about it.
On the Torus side: T35
For a considerable time I am working to find out the number for T35. My approximation formula (see article "An Easy Counting Lemma") gives a value of 9.66 quadrillions; on 7th of march, 2020, the number of 53,742,116,622,600 (ca 54 trillions) were definitely found, corresponding to 0.55 percent only of the estimated value.
General approach
The general approach is described in the paper How to search Torus N Queens solutions. Shortly and without further explanations I write it down here. The approach consists of the following points:- Compile an ordered list of the (mathematical) necklaces, or at least the first part of it. For n=35, the list consists of 342,476 necklaces which have less than 11 beads. For larger necklaces, a special handling is done (Cut, see below).
- Generate the table of possible skeletons, for these necklaces. If the number of possible skeletons is too large, for some branch, then I switch to the special handling in this case also. For n=35, I got 7,467,085 skeletons from 10,609 necklace having less than 8 beads. For larger necklaces, a special handling starts from the 28,260 necklaces of 8 beads; the handling of the program at this place allows to proceed to solutions containing larger necklaces, in the search; at all other places in the whole approach, this is avoided.
- Do the main search for the cases where the skeleton search did not continue with larger branches; I call them "Cut cases", as the search for larger skeletons was cut off. This is subdivided into small cases (more preset queens) and large cases (less preset queens).
- Filtering and sorting the solutions which exceed the proper skeleton (the start point of the search for this case), from the previous step.
- Include the additional skeletons and their solutions in the database.
- Search for the 'normal' skeletons, i.e. skeletons where branching to extensions was already done in the generation of skeletons, the second step above. This is subdivided into small and large cases, again.
- A scan over the complete database: compute symmetry factors where they are needed, and add up all data.
- Tests for the result. It is a separate point how it is planned.
The search needs much computing effort; the project is supported by Lino GmbH, which provides a virtual server, for the time not used from other application. For the rest, my computer is working on it, and it may take still a couple of years. The search is running in the background and affects other activities very little. It is easy to interrupt the search if needed and resume it later.
Chronology
- Since 2017: Development of the idea and implementation of the programs for the approach; test with smaller sizes.
- 2019-08-25: Start of n=35, search for the admissible skeletons.
- 2019-08-28: Preliminary database generated; it has 7,467,085 entries.
- 2019-10-24: The search for solutions of large necklaces (at least 8 beads) finished; 290,169,786 solutions found; they must be normalised and sorted before the database is extended.
- 2020-03-07: cut handling of the "small" cases is finished. Start of search for the large cut cases (i.e. only few preset queens).
- 2020-04-07: first search run on the Lino server starts.
- 2020-07-04: first search run on the Lino server ends successfully; the second run starts.
Special points, which I detected during the search
How to handle the skeletons?
The way for an efficient search was planned via the skeletons with respect to necklaces - of course skeletons and necklaces as mathematical terms. I also thought that a big part of the search could be done on FPGAs. Unfortunately, this is too complex for an efficient implementation on FPGAs. Therefore, the program is executed on conventional Intel-compatible PCs completely.
Meanwhile, I am thinking of another idea in parallel: do the search with line skeletons instead of necklace skeletons; I will explain it further in the future. Roughly speaking, necklace skeletons handle lines containing many queens in a predefined order; for line skeletons, the order of the queens does not matter, only the number of queens on the lines is of interest.
To find the necklace skeleton of a solution requires relatively much CPU; but perhaps I must only optimise my implementation. A different approach is to search the line skeleton first, and from it the necklace skeleton afterwards. Up to now, the search for the line skeleton is faster by a considerable factor: for T23, the factor is 244, for T25 it is 324.
The disadvantage is that there are more line skeletons than necklace skeletons. To get some impression of the numbers, I have generated diagrams showing the number of solutions, depending on the size of the skeleton, both for line and necklace skeletons.




The first solutions for "large" cases.
During the search from 3 preset queens only, the solutions below were found among others, in the first 130 hours, on the server of Lino GmbH: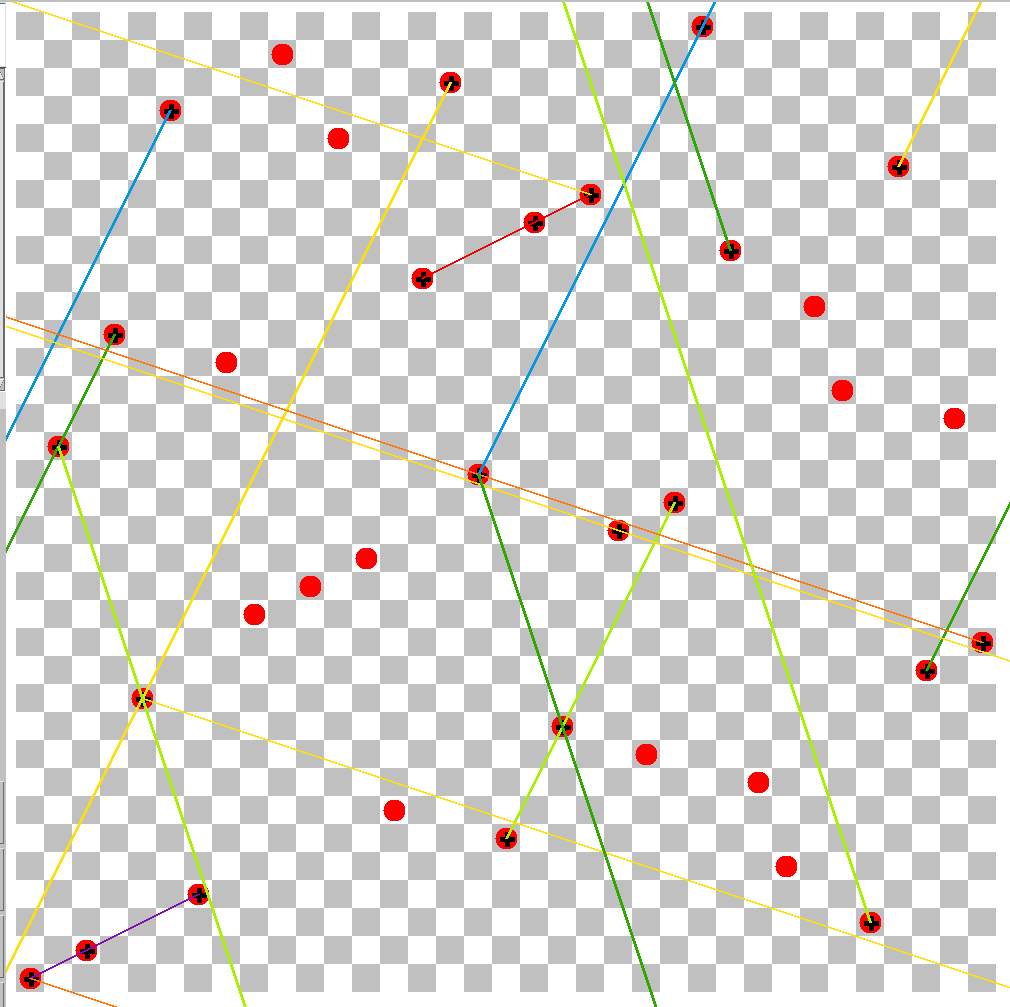

They belong to necklace 6, with beads at 0-1-3; this gives preset queens on 0/0, 2/1, and 6/3. Queens of the skeleton are marked with a black plus sign. Some colored lines show further knight lines populated with three queens in a position corresponding to the necklace. For example in the left image the queens on 17/5, 19/9, and 23/17 (bright green line). In this case, the necklace is expanded to 0-2-6 (by factor 2).
One can see also the three queens on 8/13, 10/14, and 12/15 on a knight line; but these positions belong to the smaller necklace 0-1-2, therefore the queens do not belong to the skeleton.